Barisan dan Deret Aritmatika Beserta Contohnya

Barisan dan Deret Aritmatika Beserta Contohnya – Untuk kali ini kami akan bagi materi mengenai Aritmatika yang dalam hal meliputi seperti rumus, pengertian, sifat dan contoh soal, kalau begitu simak saja uraian dibawah ini.

Daftar isi

Barisan Aritmatika

Dalam pembahasan sebelumnya, telah diketahui bahwa barisan bilangan dinyatakan dalam bentuk U1, U2, U3, U4, . . ., Un. Barisan bilangan ini disebut sebagai barisan bilangan aritmatika, jika selisih dua suku yang berurutan selalu tetap. Selisih tersebut dinamakan beda dan dilambangkan dengan “b“.

Jadi, `b=U_2-U_1=U_3-U_2=U_4-U_3=…=U_n-U_{n-1}`

Jika dalam barisan aritmatika tersebut suku pertama dinyatakan dengan a, maka bentuk umum barisan aritmatika adalah:

a, a + b, a + 2b, a + 3b, . . . , a+(n–1) b

Contoh 5.7

Terdiri atas:

1, 4, 7, 10, . . .

b = U2 – U1 = U3 – U2 = U4 – U3

b = 4 – 1 = 7 – 4 = 10 – 7 = 3

Karena barisan bilangan tersebut mempunyai beda yang tetap yaitu 3, maka barisan itu merupakan barisan aritmatika.

2, 5, 7, 9 , . . .

b = U2 – U1 = U3 – U2 = U4 – U3

U2 – U1 = 5 – 2 = 3

U3 – U2 = 7 – 5 = 2

U4 – U3 = 9 – 7 = 2

Karena barisan bilangan tersebut mempunyai beda yang tidak tetap, maka barisan tersebut bukan barisan aritmatika.

Jadi, barisan aritmatika adalah suatu barisan bilangan yang suku beriktnya diperoleh dengan menambah atau mengurangi dengan suatu bilangan yang tetap kepada suku sebelumnya. Bilangan yang tetap itu disebut selisih atau beda. Apabila bedanya positif, maka barisan itu naik. Apabila bedanya negative, maka barisan itu turun.

Menentukan Rumus Suku ke-n Barisan

Jika suku pertama U1, kita misalkan a, beda kita misalkan b, dan suku ke-n kita misalkan Un maka barisan aritmatika ditulis sebagai berikut:

Rumus suku ke-n suatu barisan aritmatika adalah Un = a + (n – 1) b

Sifat-sifat suku ke-n

Un = a + (n – 1) b = a + bn – b = bn + (a – b).

Jadi, suku ke-n suatu barisan aritmatika adalah fungsi linier dari n, dengan n bilangan asli.

Deret Aritmatika

Dari pengertian barisan bilangan pada pembahasan sebelumnya, jika semua suku-suku pada barisan aritmatika dijumlahkan akan terbentuk suatu deret aritmatika atau deret hitung. Sehingga bentuk umum deret aritmatika adalah:

a+(a+b)+(a+2b)+(a+3b)+…+{a+(n-1)b}

Deret aritmatika yang mempunyai beda lebih dari nol atau positif, maka deretnya disebut deret aritmatika naik. Sedangkan deret aritmatika yang mempunyai beda kurang dari nol atau negatif, maka deretnya disebut deret aritmatika turun.

Baca juga: Pertidaksamaan Linear Satu Variabel

Contoh 5.8

Terdiri atas:

Apakah 2 + 5 + 8 + 11 + 14 + 17 + . . . deret aritmatika?

U2 – U1 = 5 – 2 = 3 → U4 – U3 = 11 – 8 = 3

U3 – U2 = 8 – 5 = 3 → U5 – U4 = 14 – 11 = 3

Karena bedanya selalu tetap yaitu 3, maka 2 + 5 + 8 + 11 + 14 + 17 + . . . adalah deret aritmatika atau deret hitung.

Apakah 2 + 6 + 10 + 14 + 18 + . . . deret aritmatika?

U2 – U1 = 6 – 2 = 4 → U4 – U3 = 14 – 10 = 4

U3 – U2 = 10 – 6 = 4 → U5 – U4 = 18 – 14 = 4

Karena bedanya selalu tetap yaitu 4, maka 2 + 6 + 10 + 14 + 18 + . . . adalah deret aritmatika atau deret hitung.

a. Rumus Suku ke-n Deret Aritmatika

Apabila a menyatakan suku pertama, n menyatakan banyak suku, dan b adalah beda suatu barisan aritmatika, maka:

U1 = a

U2 = a + b

U3 = a + 2b

. . .

Un = a + (n – 1)b

Jadi, suku ke-n barisan aritmatika (Un) dirumuskan sebagai:

`U_n = a+(n-1)b`

b. Jumlah n Suku Pertama Deret Aritmatika

Untuk memudahkan perhitungan, berikut ini akan dicari rumus menentukan jumlah n suku pertama deret aritmatika.

U1 = a

U2 = a + b

U3 = a + 2b

. . .

Un = a + (n – 1)b

—————————————————————-+

Sn = a + a + a + . . . + b + 2b + 3b + . . . + (n–1) b

Sn = na + b + 2b + 3b + . . . + (n–1) b

= na + {(1 + 2 + 3 + . . . + (n–1)}b

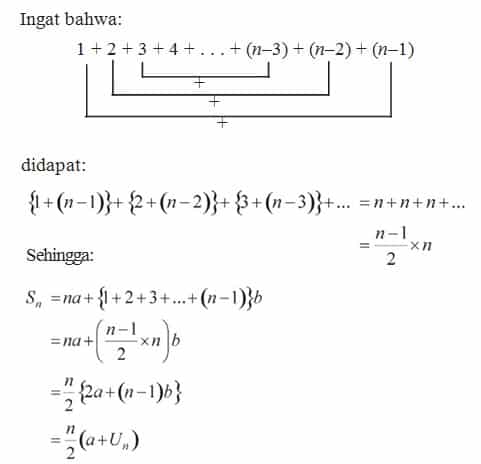
Jadi, rumus jumlah n suku pertama deret aritmatika adalah:

`S_n=n/2{2a+(n-1)b}` atau `S_n=n/2(a+U_n)`

c. Suku Tengah Deret Aritmatika

Dalam deret aritmatika jika n ganjil, maka suku tengah (Ut) deret aritmatika tersebut terletak di tengah-tengah antara U1 dan Un dan dirumuskan sebagai:

`U_t=1/2(a+U_n)`

d. Sisipan pada Deret Aritmatika

Misalkan U1 + U2 + U3 + U4 + . . . + Un adalah deret aritmatika dengan suku pertama U1 = a, beda = b, dan banyaknya suku = n.Apabila di antara dua suku deret aritmatika tersebut disisipkan k buah bilangan (suku baru) sehingga membuat deret aritmatika baru, maka:

Deret semula:

`a+(a+b)+(a+2b)+…`

Deret baru:

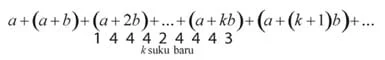
Dari deret semula dan deret baru diperoleh hubungan:

Beda baru (b‘)

`b’=b/{k+1}`

Banyaknya suku baru (n‘)

`n’=n+(n+1)k`

Jumlah n suku pertama sesudah sisipan (Sn‘)

`S_n’={n’}/2(a+U_{n’})`

Sifat-Sifat Deret Aritmatika

Masih ingatkah kita dengan rumus suku ke-n dan jumlah n suku pertama pada deret aritmatika? Nah, dari rumus suku ke-n dan jumlah n suku pertama pada deret aritmatika tersebut kita akan menemukan sifat-sifat deret aritmatika.

Baca juga: Pengertian Besaran, Satuan, dan Pengukuran

Bentuk umum dari suatu deret aritmatika adalah:

a+(a+b)+(a+2b)+…+{a+(n-1)b}

Berikut ini akan diuraikan beberapa sifat lain pada deret aritmatika.

Misalkan diketahui deret aritmatika 2 + 6 + 10 + 14 + 18 + . . . , a = 2, b = 4

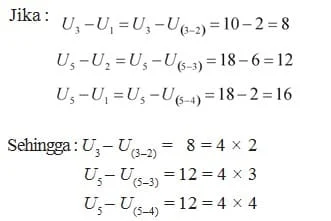
Dari uraian di atas maka:

`U_n-U_{(n-p)}=bxp` ……………………….. (sifat 1)

Dalam pembahasan sebelumnya telah kita ketahui bahwa:

`S_n=n/2(a+U_n)=n/2{2a+(n-1)b}` ……………. (sifat 2)

Jika banyak suku barisan aritmatika ganjil dan suku tengahnya adalah Ut maka:

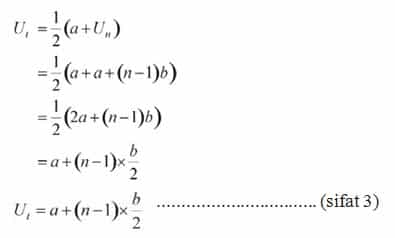
Hubungan antara Sn dan Un

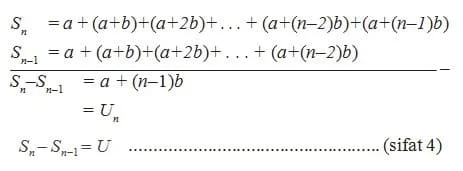
Contoh Soal Deret Aritmatika Beserta Jawabannya

Berikut ini terdapat beberapa contoh soal deret aritmatika beserta jawabannya, terdiri atas:

1. Suku ke4 dan suku ke9 suatu barisan aritmatika berturutturut adalah 110 dan 150. Suku ke30 barisan tersebut adalah …

Pembahasan

Dari beberapa suku yang diketahui diperoleh persamaan yaitu :

(1) U4 = a + 3b = 110

(2) U9 = a + 8b = 150

Dengan dua persamaan di atas, kita dapat menentukan nilai suku pertama (a) dan beda (b) barisan aritmatika tersebut. Nilai a dan b dapat ditentukan dengan metode eliminasi ataupun metode substitusi. Dengan metode substitusi, diperoleh :

a + 3b = 110 → a = 110 3b → substitusi ke persamaan (2).

a + 8b = 150

⇒ 110 3b + 8b = 150

⇒ 110 + 5b = 150

⇒ 5b = 40

⇒ b = 8

Karena b = 8, maka a = 110 3(8) = 110 24 = 86. Jadi, suku ke30 barisan aritmatika tersebut adalah : U30 = a + 29b

⇒ U30 = 86 + 29(8)

⇒ U30 = 86 + 232

⇒ U30 = 318 (Opsi B)

2. Dari suatu barisan aritmatika diketahui suku ke5 adalah 22 dan suku ke12 adalah 57. Suku ke15 barisan ini adalah …

Pembahasan

Dari soal diperoleh dua persamaan sebagai berikut :

(1) U5 = a + 4b = 22

(2) U12 = a + 11b = 57

Dengan menggunakan metode substitusi, diperoleh nilai suku pertama dan beda sebagai berikut :

a + 4b = 22 → a = 22 4b → substitusi ke persamaan (2). a + 11b = 57

⇒ 22 4b +11b = 57

⇒ 22 + 7b = 57

⇒ 7b = 35

⇒ b = 5

Karena b = 5, maka a = 22 4(5) = 22 20 = 2.

Jadi, suku ke15 barisan aritmatika tersebut adalah : U15 = a + 14b

⇒ U15 = 2 + 14(5)

⇒ U15 = 2 + 70

⇒ U15 = 72 (Opsi C)

3. Suku keempat dan suku ketujuh suatu barisan aritmatika berturutturut adalah 17 dan 29. Suku barisan ke25 adalah …

Pembahasan

Dari soal diperoleh dua persamaan sebagai berikut :

(1) U4 = a + 3b = 17

(2) U7 = a + 6b = 29

Dengan menggunakan metode substitusi, diperoleh nilai suku pertama dan beda sebagai berikut :

a + 3b = 17 → a = 17 3b → substitusi ke persamaan (2). a + 6b = 29

⇒ 17 3b + 6b = 29

⇒ 17 + 3b = 29

⇒ 3b = 12

⇒ b = 4

Karena b = 4, maka a = 17 3(4) = 17 12 = 5.

Jadi, suku ke25 barisan aritmatika tersebut adalah : U25 = a + 24b

⇒ U25 = 5 + 24(4)

⇒ U25 = 5 + 96

⇒ U25 = 101 (Opsi B)

4. Suku kedua barisan aritmatika adalah 5 dan suku kelima adalah 14. Suku ke20 barisan aritmatika tersebut adalah …

Pembahasan

Dari soal diperoleh dua persamaan sebagai berikut :

(1) U2 = a + b = 5

(2) U5 = a + 4b = 14

Dengan menggunakan metode substitusi, diperoleh nilai suku pertama dan beda sebagai berikut :

a + b = 5 → a = 5 b → substitusi ke persamaan (2). a + 4b = 14

⇒ 5 b + 4b = 14

⇒ 5 + 3b = 14

⇒ 3b = 9

⇒ b = 3

Karena b = 3, maka a = 5 3 = 2.

Jadi, suku ke20 barisan aritmatika tersebut adalah : U20 = a + 19b

⇒ U20 = 2 + 19(3)

⇒ U20 = 2 + 57

⇒ U20 = 59 (Opsi A)

5. Dari suatu barisan aritmatika diketahui suku keempat adalah 7 dan jumlah suku keenam dan kedelapan adalah 23. Besar suku kedua puluh adalah …

Pembahasan

Dari soal diperoleh dua persamaan sebagai berikut :

(1) U4 = a + 3b = 7

(2) U6 + U8 = (a + 5b) + (a + 7b) = 2a + 12b = 23

Dengan menggunakan metode substitusi, diperoleh nilai suku pertama dan beda sebagai berikut :

a + 3b = 7 → a = 7 3b → substitusi ke persamaan (2).

2a + 12b = 23

⇒ 2(7 3b) + 12b = 23

⇒ 14 6b + 12b = 23

⇒ 6b = 9

⇒ b = 9/6 = 3/2

Karena b = 3/2, maka a = 7 3(3/2) = (14 9)/2 = 5/2. Jadi, suku ke20 barisan aritmatika tersebut adalah : U20 = a + 19b

⇒ U20 = 5/2 + 19(3/2)

⇒ U20 = 5/2 + 57/2

⇒ U20 = 62/2 = 31 (Opsi C)

Demikianlah pembahasan mengenai Barisan dan Deret Aritmatika Beserta Contohnya semoga dengan adanya ulasan tersebut dapat menambah wawasan dan pengetahuan anda semua

Barisan dan Deret Aritmatika Beserta Contohnya