Rumus Standar Deviasi – Dalam statistika, standar deviasi adalah ukuran yang digunakan untuk mengukur jumlah variasi atau sebaran sejumlah nilai data.
Semakin rendah standar deviasi, maka semakin mendekati rata-rata, sedangkan jika nilai standar deviasi semakin tinggi maka semakin lebar rentang variasi datanya. Sehingga standar deviasi merupakan besar perbedaan dari nilai sampel terhadap rata-rata.
Daftar isi
Pengertian Standar Deviasi
Standar deviasi adalah nilai statistik yang dimanfaatkan untuk menentukan bagaimana sebaran data dalam sampel, serta seberapa dekat titik data individu ke mean atau rata-rata nilai sampel.
Untuk cara menghitung standar deviasi, yang perlu dilakukan pertama-tama adalah menghitung nilai rata-rata dari semua titik data. Rata-rata sama dengan jumlah dari semua nilai dalam kumpulan data lalu dibagi dengan jumlah total titik data tersebut.
Setelah itu langkah berikutnya adalah menghitung penyimpangan setiap titik data dari rata-rata. Caranya dengan mengurangkan nilai dari nilai rata-rata. Deviasi setiap titik data akan dikuadratkan dan dicari penyimpangan kuadrat individu rata-rata. Lalu nilai yang dihasilkan disebut sebagai varians. Sedangkan standar deviasi adalah akar kuadrat dari varians.
Fungsi Standar Deviasi
Biasanya standar deviasi dimanfaatkan oleh para ahli statistik atau orang yang berkecimpung dalam dunia tersebut untuk mengetahui apakah sampel data yang diambil mewakili seluruh populasi.
Sebab mencari data yang tepat untuk suatu populasi sangat sulit untuk dilakukan. Maka dari itu perlu menggunakan sampel data yang dapat mewakili seluruh populasi sehingga mempermudah untuk melakukan penelitian atau suatu tugas.
Sebagai gambaran, jika seseorang ingin mengetahui berat badan anak laki-laki berusia 10-12 tahun di suatu sekolah, maka yang perlu dilakukan adalah mencari tahu berat beberapa orang dan menghitung rata-rata serta standar deviasinya. Dari perhitungan tersebut akan diketahui nilai yang dapat mewakili seluruh populasi.
Baca juga: Teorema Pythagoras: Rumus dan Penjelasannya
Rumus Standar Deviasi
Dalam menghitung standar deviasi, ada beberapa metode yang bisa dimanfaatkan. Seperti menghitungnya secara manual, dengan kalkulator dan Excel. Akan kami jelaskan satu per satu. Tetapi untuk pertama-tama kita bahas cara yang manual.
Untuk mengetahui cara menghitung standar deviasi maka ada dua rumus yang harus diketahui, yakni rumus varian dan rumus standar deviasi. Berikut adalah rumus yang bisa dipakai:

Keterangan:
s2 : Varian
s : Standar deviasi
xi : Nilai x ke-i
x : Rata-rata
n : Ukuran sampel
Rumus Standar Deviasi Excel
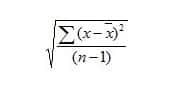
Keterangan:
x = data ke n
x bar = x rata-rata = nilai rata-rata sampel
n = banyaknya data
Rumus Standar Deviasi Gabungan
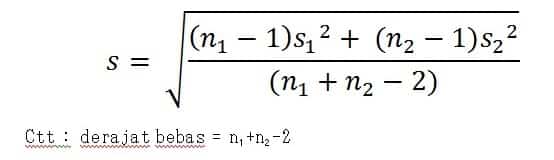
Cara Menghitung Standar Deviasi
Berikut ini terdapat beberapa cara menghitung standar deviasi, terdiri atas:
Cara Menghitung Standar Deviasi Data Tunggal

Cara Menghitung Standar Deviasi Excel
STDEV (number1, number2,…)
Dengan :
Number1, number2, … adalah 1-255 argumen yang sesuai dengan sampel populasi. Anda juga dapat menggunakan array tunggal atau referensi ke array, bukan argumen yang dipisahkan oleh koma.
Keterangan:
- STDEV mengasumsikan bahwa argumen adalah contoh dari populasi. Jika data anda mewakili seluruh populasi, untuk menghitung deviasi standar menggunakan STDEVP.
- Standar deviasi dihitung menggunakan metode “n-1” .
- Argumen dapat berupa nomor atau nama, array, atau referensi yang mengandung angka.
- Nilai-nilai logis dan representasi teks dari nomor yang Anda ketik langsung ke daftar argumen akan dihitung.
- Jika argumen adalah sebuah array atau referensi, hanya nomor/angka dalam array atau referensi yang akan dihitung. Sel kosong, nilai-nilai logis, teks, atau nilai-nilai kesalahan dalam array atau referensi akan diabaikan.
- Argumen yang kesalahan nilai atau teks yang tidak dapat diterjemahkan ke dalam nomor/angka akan menyebabkan kesalahan. g. Jika Anda ingin memasukkan nilai-nilai logis dan representasi teks angka dalam referensi sebagai bagian dari perhitungan, gunakan fungsi STDEVA.
Cara Menghitung Standar Deviasi Gabungan
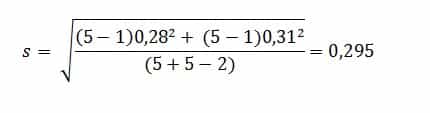
Contoh Soal Standar Deviasi
Berikut ini terdapat beberapa contoh soal dari standar deviasi, terdiri atas:
Contoh No. 1
Data umur berbunga (hari) tanaman padi varietas Pandan Wangi adalah sbb: 84 86 89 92 82 86 89 92 80 86 87 90
Berapakah standar deviasi dari data di atas?
| Sampel | y | y2 |
| 1 | 84 | 7056 |
| 2 | 86 | 7396 |
| 3 | 89 | 7921 |
| 4 | 92 | 8464 |
| 5 | 82 | 6724 |
| 6 | 86 | 7396 |
| 7 | 89 | 7921 |
| 8 | 92 | 8464 |
| 9 | 80 | 6400 |
| 10 | 86 | 7396 |
| 11 | 87 | 7569 |
| 12 | 90 | 8100 |
| Jumlah | 1043 | 90807 |
Maka nilai standar deviasi data di atas adalah:
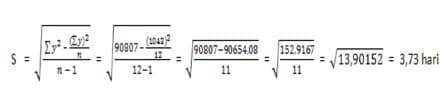
Baca juga: Pertidaksamaan Linear Satu Variabel
Contoh Soal No. 2
Data nilai 70 orang mahasiswa Statistika:

Contoh Soal No. 3
1. Buat tabel yang berisi data (Anda bisa menggunakan data yang tidak berurut dari nilai kecil ke besar)
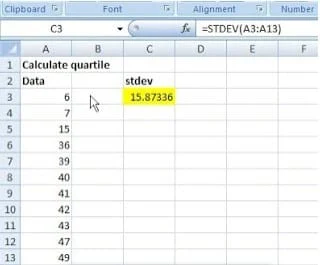
2. Untuk menghitung standard deviasi , di sel C3 ketik formula berikut :
=STDEV(A3:A13)
Catatan: Jika data anda lebih dari 11 item, cukup ganti range A3:A13





Tinggalkan Balasan